送信機のテスト回路を作ってみました。受光素子を使ってみたくなったからです。うまくやればこれでセンサ、無線通信ができるはずです。
作ったもの
作ったものは受信チェッカーです。赤外線受信素子を使用したごく簡単な構成の回路をブレットボードに刺しただけなので作った感は薄いですが。この回路は送信機や受光素子のテストに使えます。
機能
- 4.5~5.5V電源
- 受光素子が対応している変調周波数の赤外線を受信するとLEDが点滅する。
動作


テスト用の送信機はテレビのリモコンを使いました。どこのメーカーのも大体FM38kHzらしいです。
狭い室内でやったところ、光が反射するので360度反応しました。机の下でも大丈夫! だだし経路が目測3mくらいまでで、4mくらいになるとまっすぐ向けていても反応しませんでした。送信機の電力を大きくすると伸びる?かもしれない。送信機を作ったらやってみます。
材料

- 赤外線受光素子PL-IRM0101 1 38kHzを受信するとVoutがVccから0V(HighからLow)に落ちます。
- pnpトランジスタ 2SA1015
- 発光ダイオード 持ってたやつ 1
- 抵抗器 22kΩ 220Ω 1つずつ
- コンデンサ 22μF
- 電池ソケットと乾電池3つ
4.5~5.5V電源なら何でもいいです。乾電池3つでは一般的に4.5Vです。電圧を測ってみたら4.8Vでした。
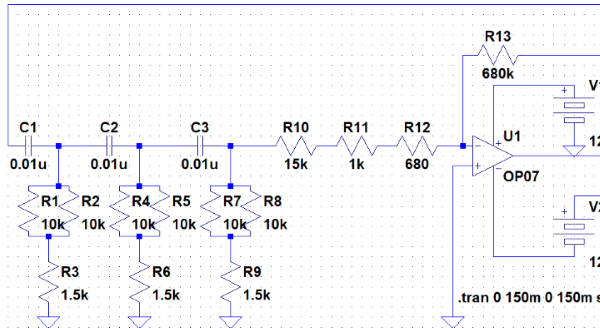
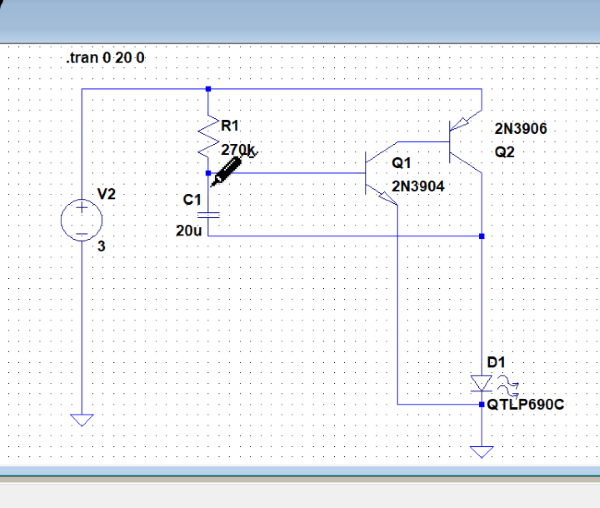
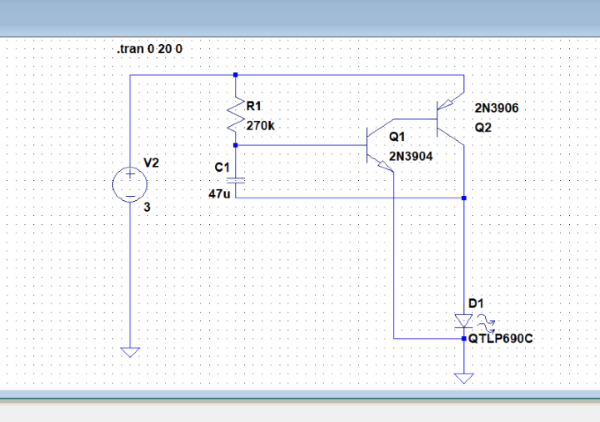
回路
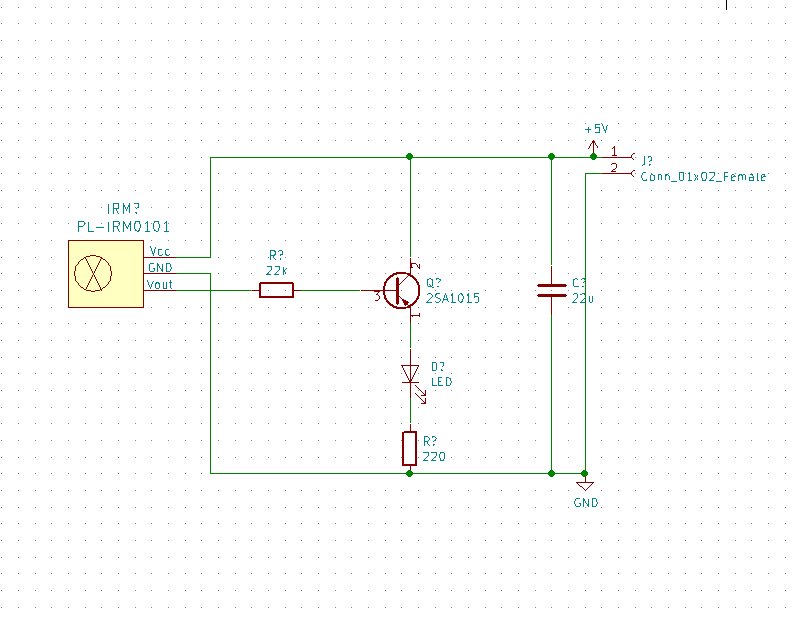
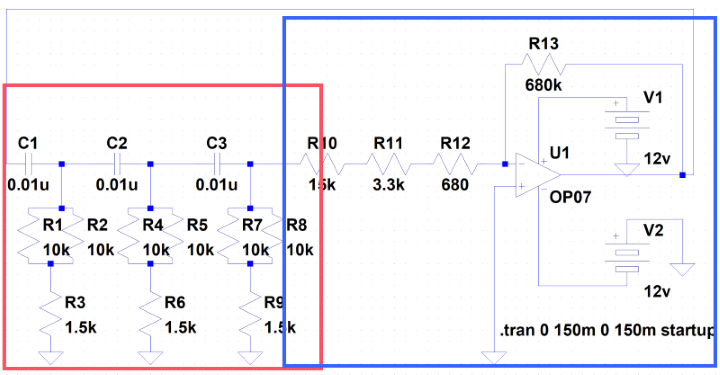
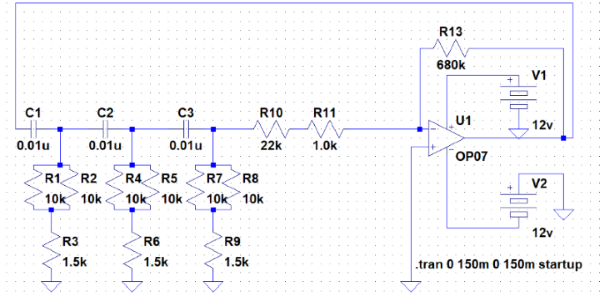
回路は上記の通りです。参考の本のまんまです。
使用センサの電源が4.5V~5.5Vだったので、5V電源と書いています。端っこのJがバッテリにつながるコネクタです。回路としてイメージしやすいようにできればと書き加えたものです。実際には私はこれに電池ソケットと電池3本4.5V をつなぎました。
以下は回路の解釈です。
この回路は基本的なスイッチング回路です。スイッチング回路とは、トランジスタの「ベースに条件を満たす電圧がかかった時にエミッタコレクタ間に電流が流れる」という特性をスイッチとして利用した回路です。ここで使用している2SA1015はpnp型のトランジスタですので、電圧がしきい値以下(OFF)の時にスイッチがONになります。
ここで使用しているフォトダイオードは赤外線を受講しているときOFF、していないときONになるように作られています。なので、赤外線を受信したときにスイッチがONになります。
22kΩ抵抗はベース電流を抑えるためのものです。Voutが5Vの時、ベース電圧が4.3Vくらいなので、
$$ \frac{V}{R} = \frac{4.3[V]}{22k[Ω] }\simeq 0.195 [mA] $$
だいたい0.2mAになります。一方で、2AS1015、LED、220Ω抵抗のループを見ると、大雑把にLEDで2Vの電圧降下があるとしたとき
\begin{equation} \frac{V}{R} = \frac{3[V]}{220[Ω]} =13.6 [mA] \end{equation}
なので、LEDには14mAくらい流れると思います。LEDは電流が多く流れるほど明るく光りますので、電流調整用です。
右端のコンデンサはバイパスコンデンサです。コンデンサは直流は通さないが交流は通すという特徴があります。詳細は下に書きました。ノイズは交流なので、直流回路で発生するノイズの交流信号を流してGNDに逃がしたり、電源を外した時にすぐに電圧がゼロにならないように緊急用電源としてついています。ICを使っているとき、ノイズや電源が急になくなることが故障の原因になるかもしれないからです。導線を使っている限りリアクタンス(コイル成分) は発生してしまうんですが、これは電流変化に応じて機電圧が生じるので、急に電圧がゼロになると予期せぬ動きをしかねません。
コンデンサの電圧、電流についてです。電圧Vは電荷量Qに比例しますので、キャパシタンスCを用いて
\begin{equation} Q = CV \end{equation}
\begin{equation} i = \frac{dQ}{dt} = C\frac{dv}{dt} \end{equation}
と書けます。小文字のi,vは交流であることが多いので、慣例に従ってみました。微分は微小時間あたりの微小変化です。例えばここに正弦波V=Acos(ωt)をいれるとコンデンサ電流IはI=Aωsin(ωt)=Aωcos(ωt+π/2)になるので、ちょこっと波長が遅れるわけです。
ここでωは各周波数で、周波数fとはω=2πfという関係があります。コンセントの電圧は東日本ではf=60Hzです。一方、直流はこの各周波数が0ですので、コンデンサの電流は下のようになって流れません。
\begin{equation} i =C\frac{dv}{dt} = C 0 = 0 \end{equation}
確かに変化分がなければただの2枚の板ですもんね。初めて知ったときはコペルニクス的回転って感じでした。そういうのって回路記号にも表れていて、FETとMOSトランジスタの記号の違いとかも面白いですね。
フォトダイオード
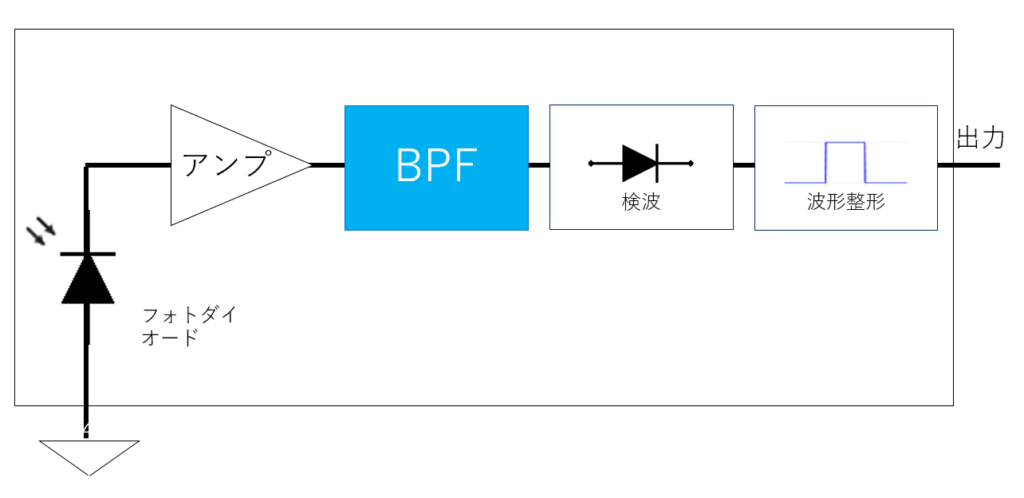
受光素子の中身はどれもだいたいこんな感じみたいです。フォトダイオードの出力をアンプで増幅し、波形を整えて全体の出力とします。今回使った素子は、出力の直前でHigh信号とLow信号を反転させていました。
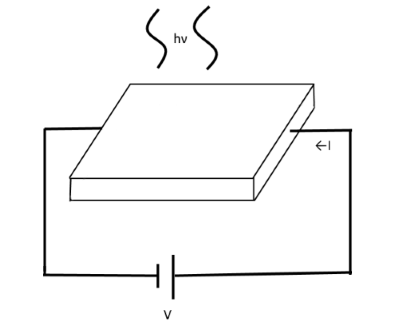
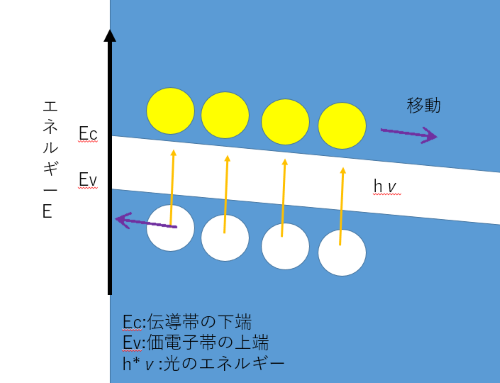
半導体のバンドギャップ以上のエネルギーをもつ光が照射されると、光導電効果を起こして電子と正孔が動き、電流が流れます。 図7は上下に粒子のエネルギーの大きさを、左右に位置を表しています。光にエネルギーを貰うと電子は伝導体に入って移動します。電子がなくなった部分を正孔と言います。
このあたりはよくご存じの方には説明する必要は無いので、初めてこういう原理を知る方が読んでもイメージできる様に書いたつもりですが、かなり雑なので気になった方は参考に乗せた本や詳しいサイトで調べてみることをおすすめします。
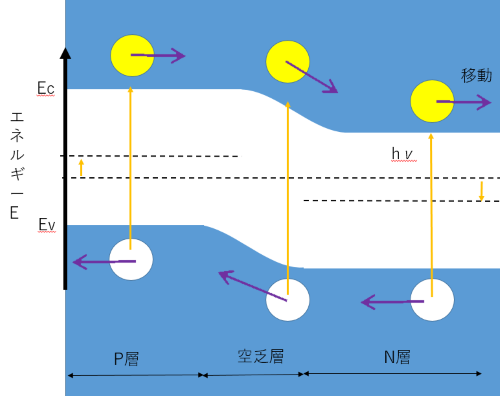
似たような効果で光起電力効果というのがあります。 n型半導体とp型半導体が接着されているもの(pn接合)に光が照射されると、半導体内部で同じように(違うといえば違うけど)電子と正孔が動き、電子はP層からn層へ、さらに外部回路へ出ていきます。 まとめると、光で電が流れるようになるので光スイッチのような感じで使えます。
雑談
最近思うのが、教科書として大学で推薦されている本って自分で確かめなくていいからとてもありがたい。本によっては完全に間違ってるものもあるじゃないですか、コードをそのまま書いても動かないとか。私がお世話になってる方の本も似たようなことがあって、それは編集の方のミスらしいです。他にも先生が自分の授業で推薦しようとしていた本をボツにした理由を話していたのを聞いたことがあります。筆者本人の認識が完全に間違っていることもありますし。という訳で、本はちゃんと能動的に確かめながら読まないといけないという認識に変化しました。 下に乗っている参考の本は授業で使っている本が多いので、私が授業を受けている先生の考えでは正しいということになりますので、ちょっと安心です。
今後はいろんな本を参考にしながら文章を書いていきたいと思います。
追記(2019/3/18) 段落構成を変更しました。内容は変更ありません。
参考
新版 電子物性 松澤剛雄・高橋清・斉藤幸喜 森北出版株式会社