PICマイコンを使ってみます。使用するのはpic16f886で、windows10、MPLAB v5.10
目次
- PIC開発環境
- 回路
- コード
- 書き込み
- 動作確認
- 雑記
- 参考
PIC開発環境
ソフトウェアでコーディングした後、ライターを用いてマイコンに書き込みます。
- ソフト (MPLAB X IDE + MPLAB XC8コンパイラ)
IDEは統合開発環境で、エディタ、デバッカ、シミュレータなどほとんどのプログラムを内蔵しています。MPLAB X IDEは8bit~32bitマイコンで共通で使用できます。 コンパイラはC言語のようなコンパイラ言語をコンパイルして機械語に翻訳するプログラムです。Cコンパイラは別にインストールし、MPLAB X IDE に統合します。
私はwindows10ですが、macでもlinuxでも同様の環境でOKみたいです。
コンパイラはいくつかありますが、microchip社が比較的新しく発表したのが MPLAB XC8コンパイラです。 MPLAB IDE8.84迄のバージョンには既にHI-TECH Cが同梱されているみたいです。
・ MPLAB X IDE | Microchip Technology
・MPLAB XC Compilers| Microchip Technology
- 書き込み機(ライター)
記事によって互換品の付属のアダプタが危険っぽかったので別途用意しました。ネタバレですが、書き込み機の一部機能が壊れてました。
回路
2つLEDをつけて交互に点滅させます。 簡単で良いです。実験中に電源が入っているかを確認するためのLEDと、電源を外したときに瞬間的にマイコン電源がなくなるのを防ぐために (一応)つけているコンデンサが加わっています。
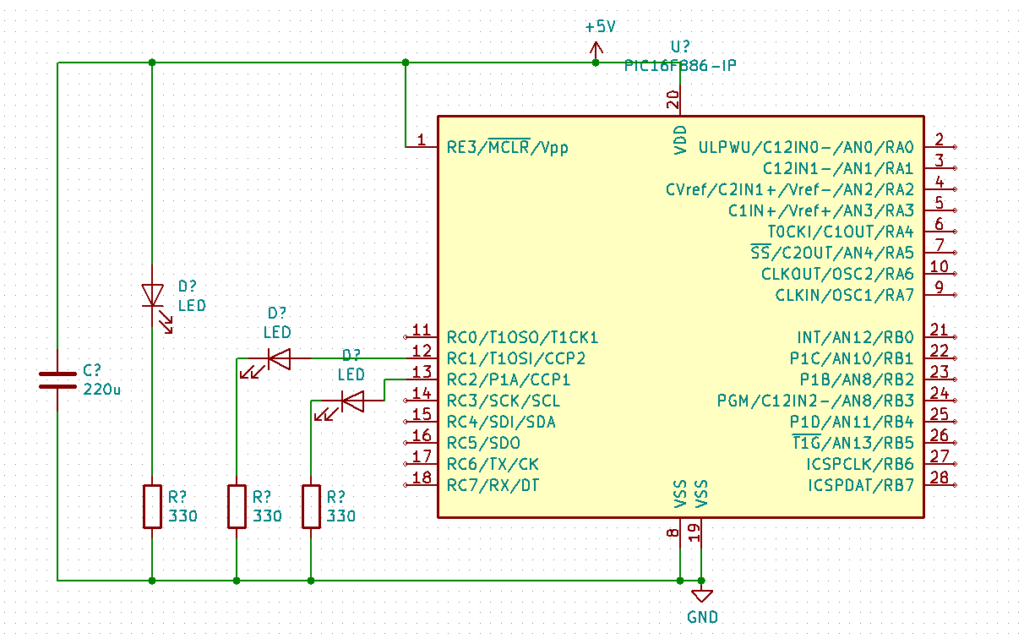
データシートを見ながら回路を組み立てます。リンクは秋月さんのとこのです。

コード
PICに書きこむ例としてリモコンのコードを見ながら、自分でコードを書いていきたいと思います。
プロジェクト
file/New Projectから作成します。MicrochipのStandalone Projectを選択します。
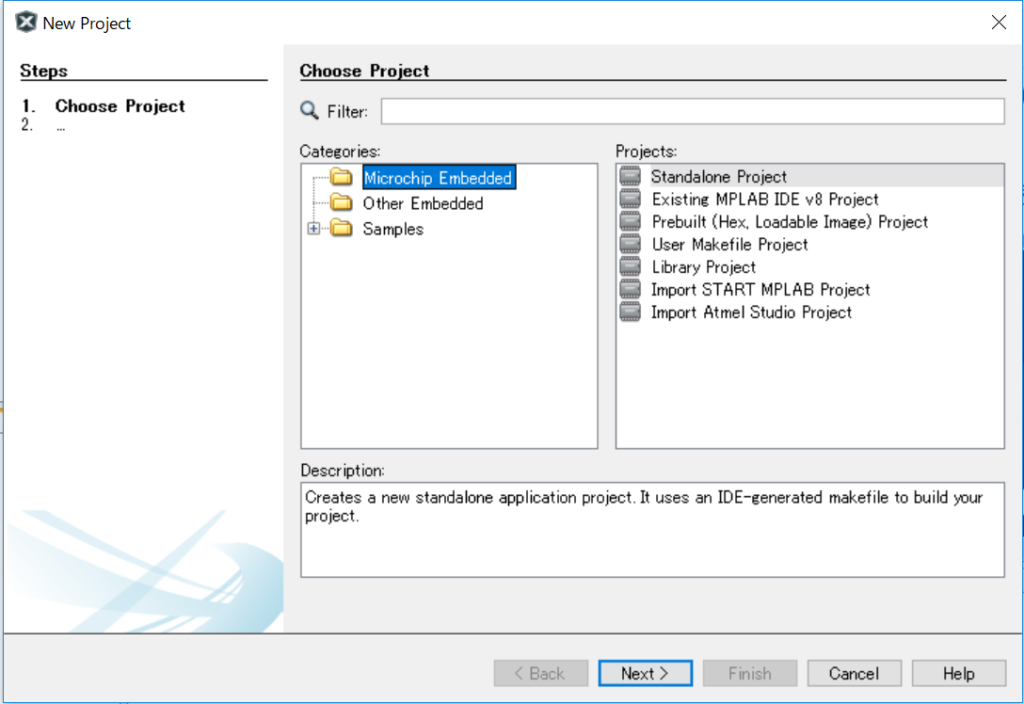
今回使うpic16f886を選択します。
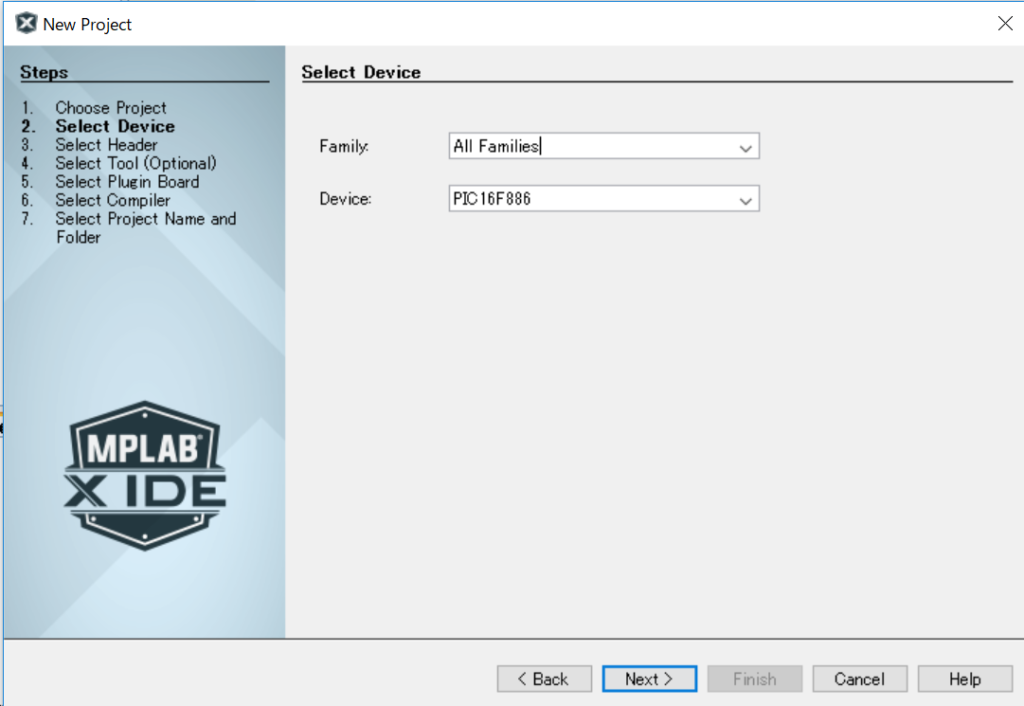
ライターは使用するPickit3を選択します。
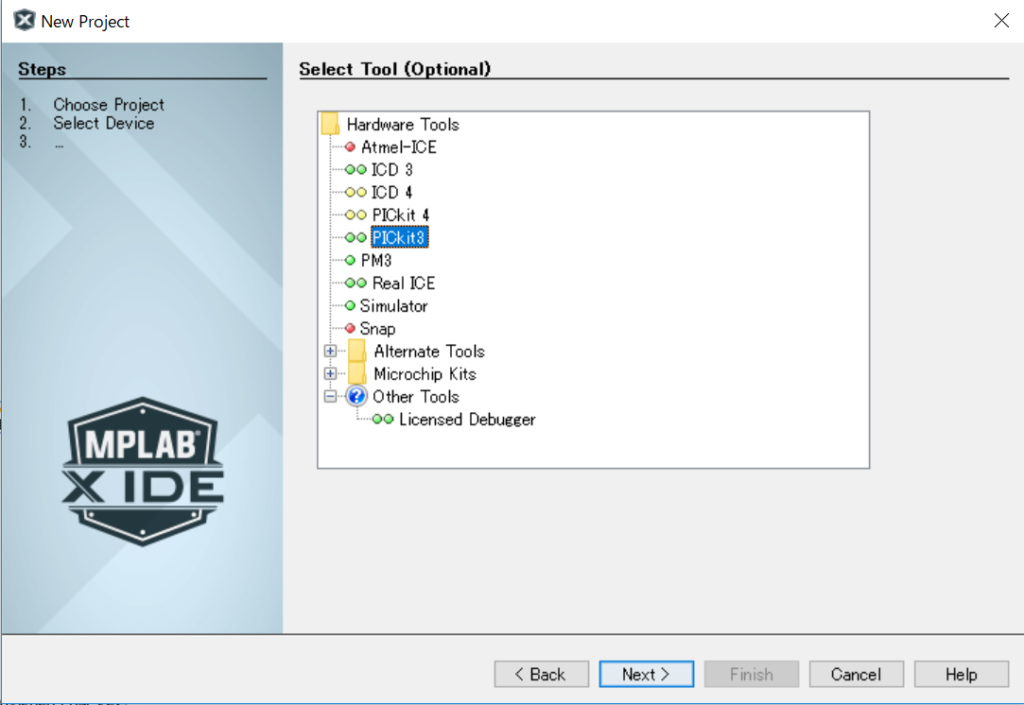
コンパイラはXC8を選択します。
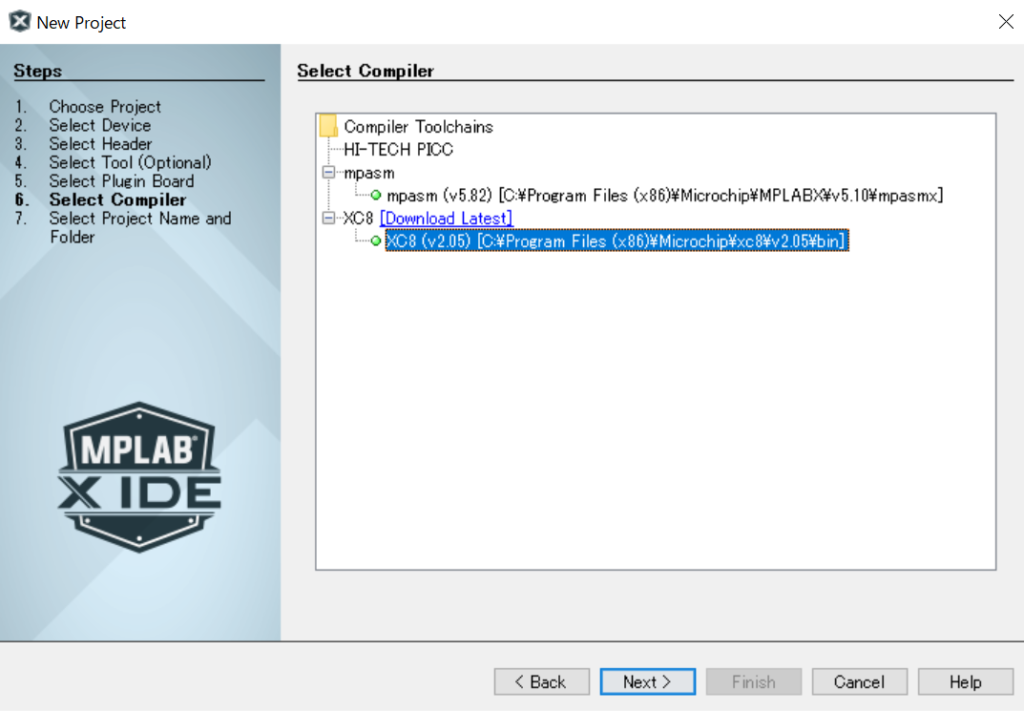
ファイル名は適当に決めます。
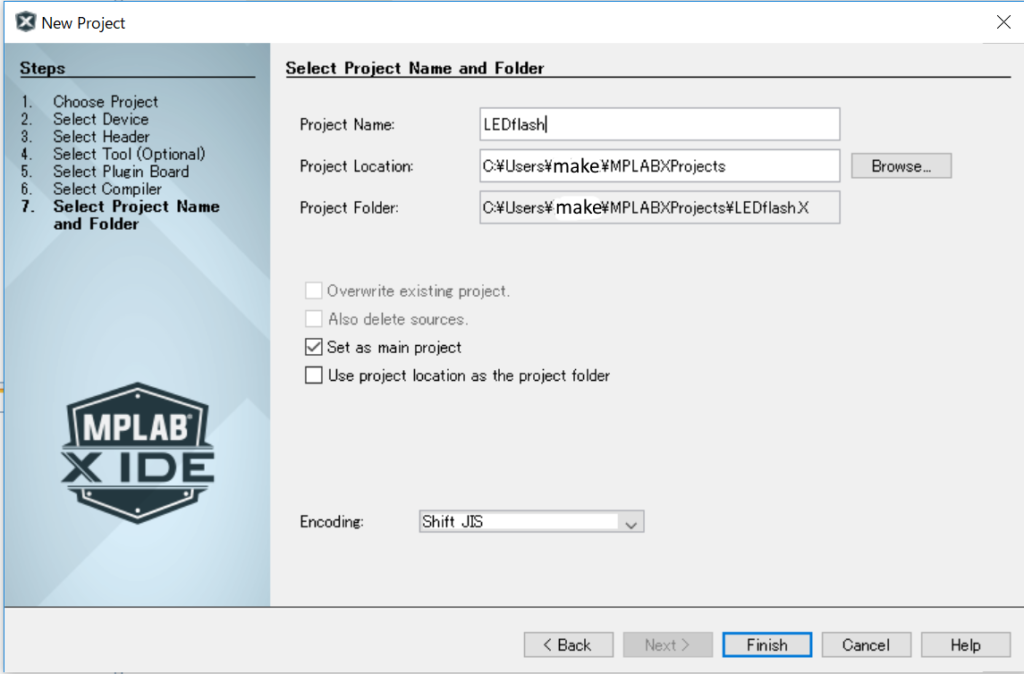
sourceフォルダの中に1つmainのファイルが必要です。
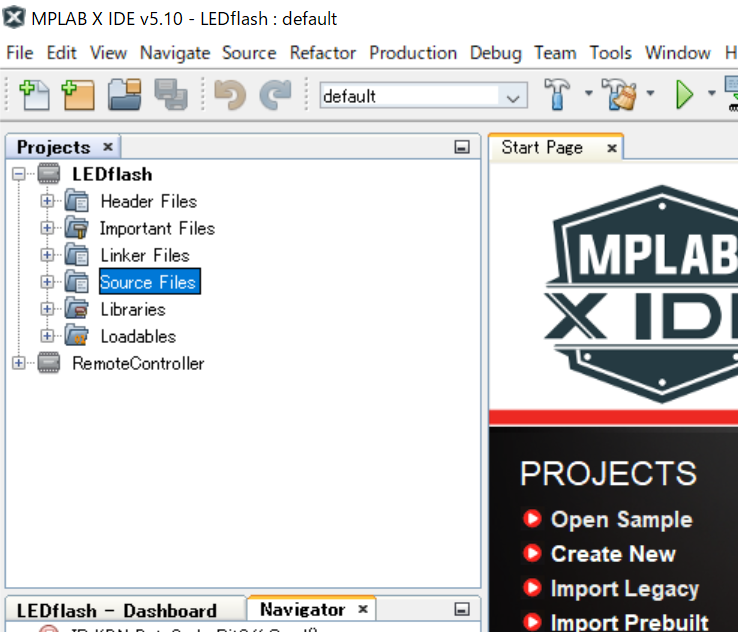
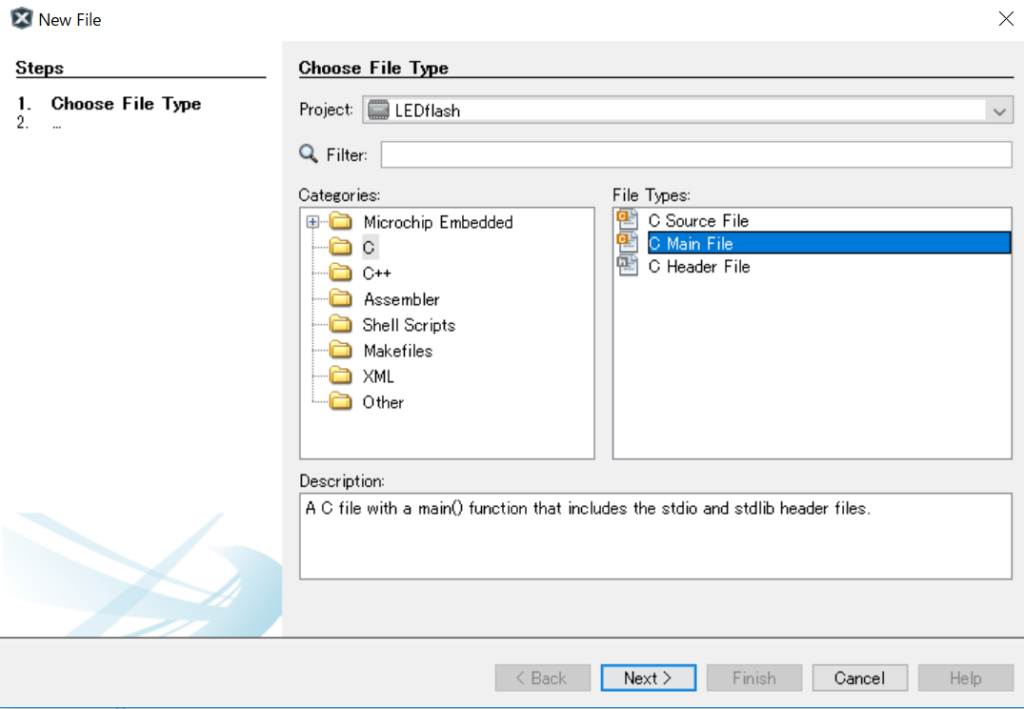
cファイルを開き、コードを書いていきます。
設定
production/set configuration bit の設定をしていきます。 なお、このマイコンはMCC対応してません。MCCは、簡単に設定できる超便利ツール、らしいです。
MPLAB® Code Configurator -microchip
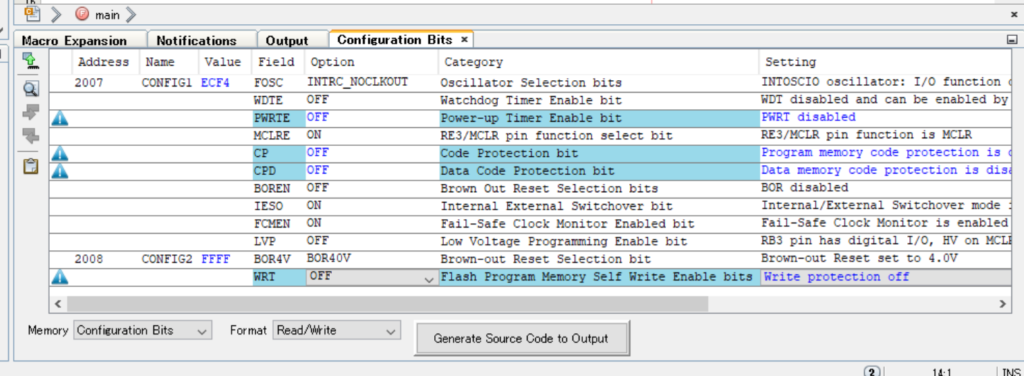
出来たら、generate source codeをクリックしてコードをコピペします。
設定は秋月のリモコンと一緒にします。今回は関数など使ってないので、I/Oさえ間違わなければ問題ないと思われます。
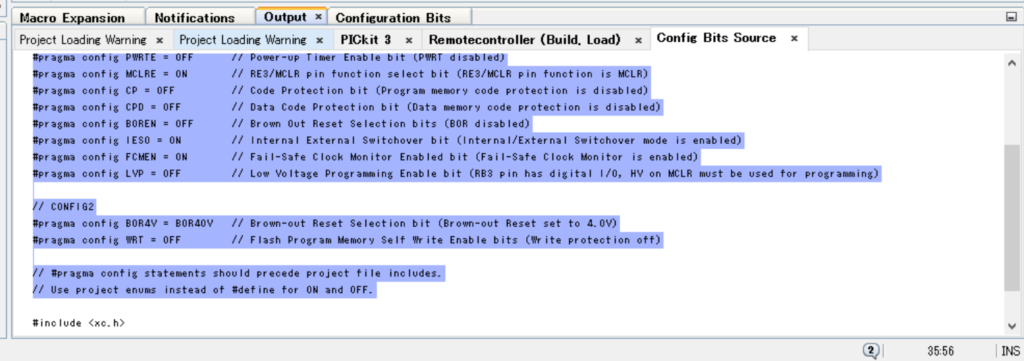
// CONFIG1
#pragma config FOSC = INTRC_NOCLKOUT // 発振回路設定 Oscillator Selection bits (INTOSCIO oscillator: I/O function on RA6/OSC2/CLKOUT pin, I/O function on RA7/OSC1/CLKIN)
#pragma config WDTE = OFF // Watchdog Timer Enable bit (WDT disabled and can be enabled by SWDTEN bit of the WDTCON register)
#pragma config PWRTE = OFF // Power-up Timer Enable bit (PWRT disabled)
#pragma config MCLRE = ON // 外部リセット/汎用入力の選択で外部リセット有効化 RE3/MCLR pin function select bit (RE3/MCLR pin function is MCLR)
#pragma config CP = OFF // Code Protection bit (Program memory code protection is disabled)
#pragma config CPD = OFF // Data Code Protection bit (Data memory code protection is disabled)
#pragma config BOREN = OFF // Brown Out Reset Selection bits (BOR disabled)
#pragma config IESO = ON // オシレータのスタートアップとコード実行の潜在時間を最小化Internal External Switchover bit (Internal/External Switchover mode is enabled)
#pragma config FCMEN = ON // オシレータの故障の場合さえ、デバイスが作動し続けるのを許容するように設計Fail-Safe Clock Monitor Enabled bit (Fail-Safe Clock Monitor is enabled)
#pragma config LVP = OFF // Low Voltage Programming Enable bit (RB3 pin has digital I/O, HV on MCLR must be used for programming)
// CONFIG2
#pragma config BOR4V = BOR40V // リセットしきい値を4V Brown-out Reset Selection bit (Brown-out Reset set to 4.0V)
#pragma config WRT = OFF // Flash Program Memory Self Write Enable bits (Write protection off)
BORとは: 事故時などに信号が不安定になるとマイコンによくありません。そこで、一定のしきい値を設定し、4Vなら4V±0.2Vを下回るとリセットを書ける機能を設定します。そのような機能をブラウンアウトリセット機能(BOR)と呼びます。
main関数
I/Oポートを設定します。クロック周期設定 I/Oポートの指定は、init関数の中で行っています。関数の使い方が解らなかったので、0~9999まで数え上げさせて時間を作る雑なコードになりました。すべてPortAの8pinすべて出力にしています。RA2=1;は、RA2が割り当てられたpinに電圧をかける指令です。
void init(){
OSCCON = 0b01110000; //8MHz
ANSEL = 0b00000000; //
TRISA = 0b00000000;//
TRISB = 0b00000000;
TRISC = 0x00;
PORTA = 0b00000000;
}
void main(void){
int i=0;
init();
while(1){
i=0;
while (i <10000){
i++;
}
RA2 = 1;
RA3 = 0;
i=0;
while (i <10000){
i++;
}
RA2 = 0;
RA3 = 1;
}
}
書き込み
繋いだらメニューバーの下の△をクリックします。

警告がでました。C:\Program Files (x86)\Microchip\xc8\v2.05\pic\includeやC:\Program Files (x86)\Microchip\xc8\v2.05\pic\include\c99に入っているヘッダファイルを開きます。私の場合はなぜかここにありましたが、多くの場合はProgram Files (x86)じゃなくProgram Filesだと思います。 C標準ライブラリ -PICマイコンによる開発手法
なんだかよく分からないままひたすら関係ありそうなヘッダファイルを開いて確認していくと、xc.hがインクルードしているalloca.hが入っていない。
MPLAB X IDE v5.xxの注意点 -サヌキテックネット にしたがって、projectのプロパティから、XC8 Global OptionsでC99をC90に変更するとビルドに成功しました。警告は無視。
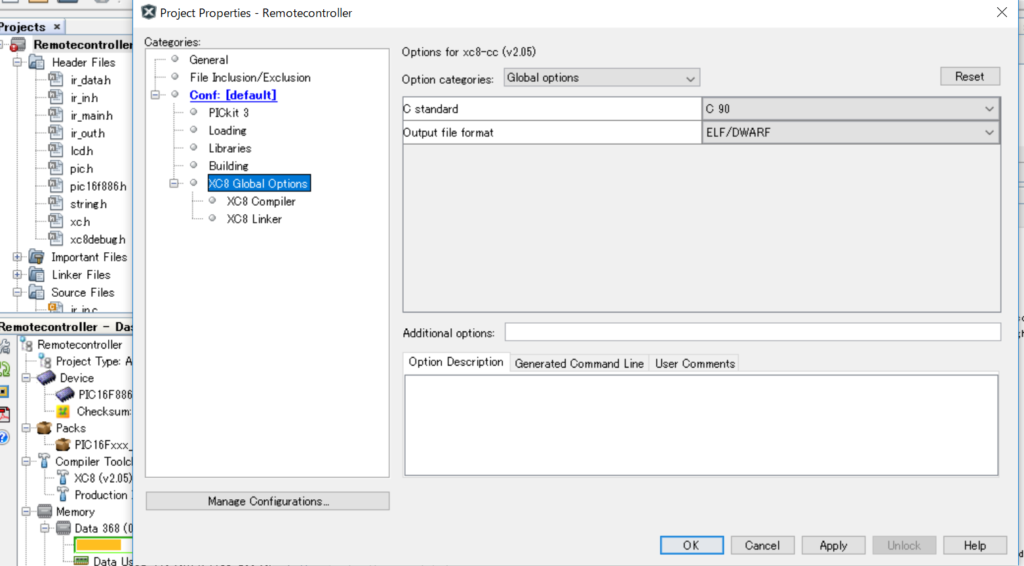
BUILD SUCCESSFUL (total time: 6s)書き込んでいきます。
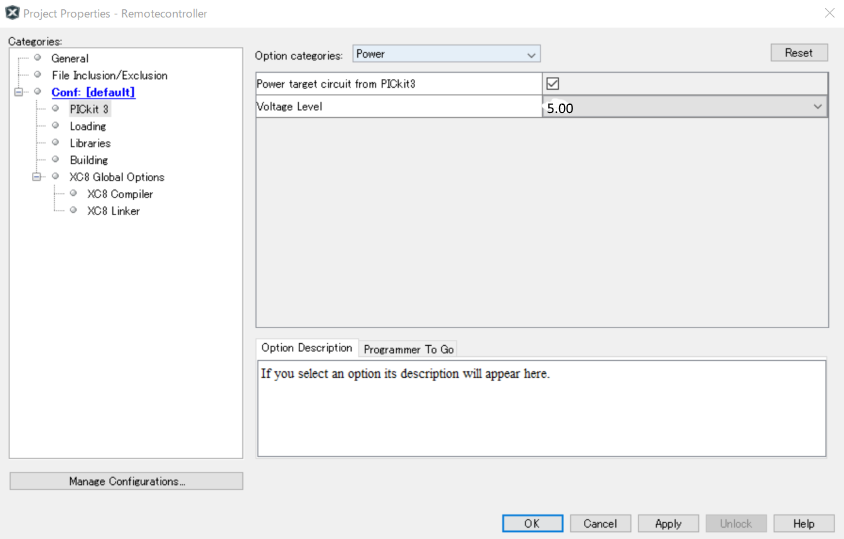
電源供給するように設定します(私のライターは安く買ったからか電源を供給する機能がうまくいきませんでした)。マイコンは電源がないと動作しませんので、ライターか回路から電源を供給して下さい。 project上右クリックでpropaties、hardware toolからPICkit3を選択、pickit3からpowerで、チェックボックスにチェック。マイコンのデータシートにWide Operating Voltage Range (2.0V-5.5V)とあったので、5.0Vの電圧を供給します。
電源がない場合はコンピュータがデバイスを見つけられない、とか、以下のようなメッセージが表示されます。
PICkit 3 is trying to supply 5.250000 volts from the USB port, but the target VDD is measured to be 4.875000 volts. This could be due to the USB port power capabilities or the target circuitry affecting the measured VDD.私はライターが壊れていたので、無理やり外部から接続できるようにしました。

Programming...
The following memory area(s) will be programmed:
program memory: start address = 0x0, end address = 0xfff
configuration memory
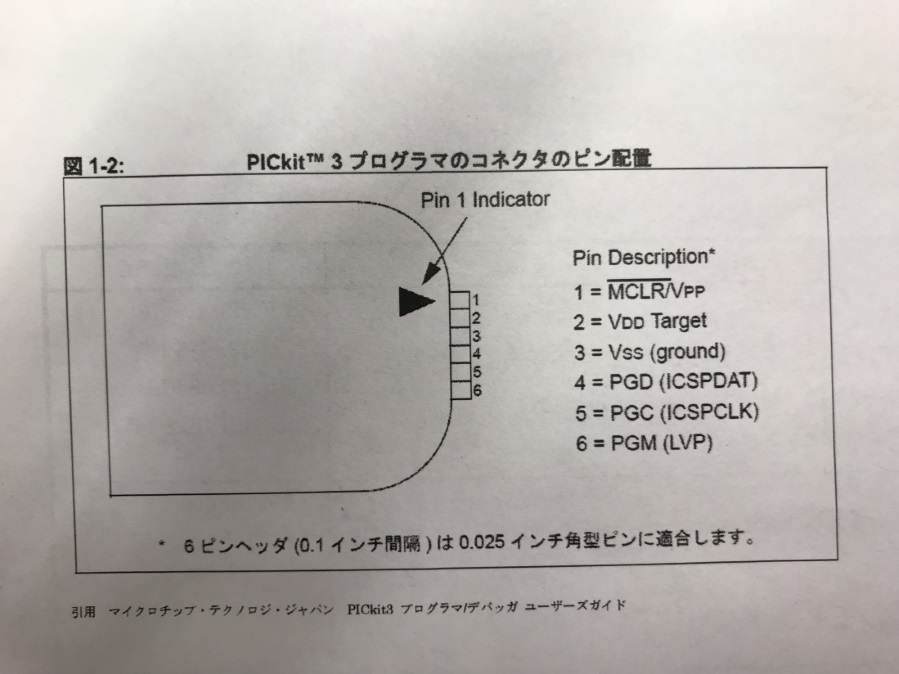
Programming/Verify completeライターの画像です。Vddに電源+、VssにGNDを接続します。(Vssは本来電源がマイナスになり得る場合のマイナス側です。)ライター付属の紙より転載。
動作確認
チカチカした。


雑談
MCCという便利機能があるんですが、Tools/Embedded/MPLAB Code Configuratorで見たところ、最新版でもサポートしているデバイスが少なく今回使用したPIC16F886もサポートされていませんでした。悲しい。