2020/04/11
本記事は学校の課題をプログラムで楽してこなそうとした際のメモを編集したものです。レポートの面影はありません。
目次
- 運動方程式を求める
- モデル
- 式変形用コード
- 運動方程式
- シミュレーションしてみる
- 順運動学、逆運動学
- 順逆動力学計算用コード
- 特異点
- 雑記
運動方程式を求める
※参考1-1のままやって一致すれば正しく出来ました、ということにしています。
モデル
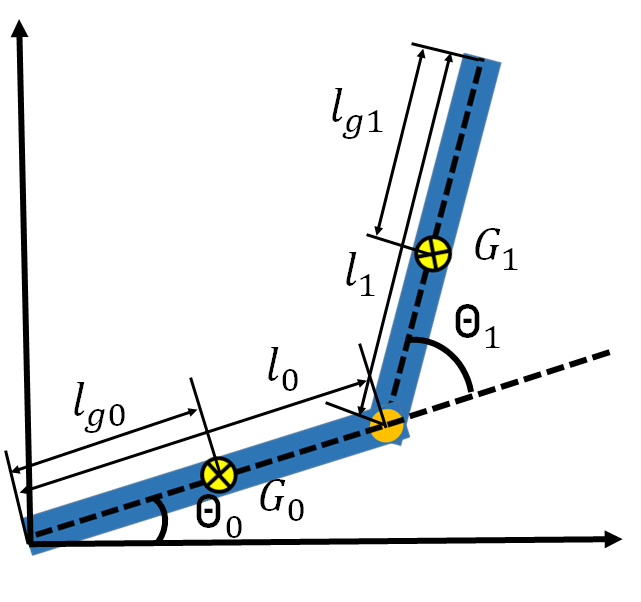
上図のような2リンクマニピュレータを考えます。G_0=(x_0,y_0), G_1=(x_0,y_1), m_0, m_1, l_0, l_1をそれぞれ第一リンク、第二リンクの重心、質量、長さとします。また、リンク端からそれぞれの重心までの長さをそれぞれl_g0, l_g1としています。
$$l_{gi}=\frac{1}{2}l_i (i=0,1)$$
ラグランジュの運動方程式に当てはめて運動方程式を求めます。
ラグランジュの運動方程式:
$$ \frac{d}{dt}(\frac{\partial L}{\partial\dot q_i})-\frac{\partial L}{\partial q_i}= Q_i (i =1,2,..,f)$$
$$L=T-U$$
あるいは、
$$ \frac{d}{dt}(\frac{\partial T}{\partial\dot q})-\frac{\partial T}{\partial q_i}+\frac{\partial U}{\partial q_i}+\frac{\partial D}{\partial \dot{q_i}}= Q_i (i =1,2,..,f)$$
L:ラグランジアン
Q:非保存力による一般化力
f:自由度
q:一般化座標
式変形用コード
ラグランジュ~でやると無限微分地獄で計算ミスのリスクが高いですね。少しの変更でものすごく時間がかかるのは嫌なので、Pythonで式変形する方法をやってみたいと思います。こういうときはmatlabっぽく書けるSimPyが便利 (雑記1.)。
- 式変形
simplify()>from sympy import *
>x, y, z = symbols('x y z')
>init_printing(use_unicode=True)
>simplify(sin(x)**2 + cos(x)**2)
1
>simplify((x**3 + x**2 - x - 1)/(x**2 + 2*x + 1))
x - 1
>simplify(gamma(x)/gamma(x - 2))
(x - 2)⋅(x - 1)式を単純化する関数で、計算量が不必要に大きくなることがあることに注意が必要です。神。
- 解く
sp.solve (Eq)引数に=0になる関数を入力します。
- 微分
diff(func, t)第二引数に何で微分するのかを入れます。
参考=>1-2、1-3、1-4
- コード
環境:
- Python 3.7.3
- numpy 1.16.4
- sympy 1.4
https://github.com/inomatly/robot_arm/blob/master/solv_lagrange.ipynb
一応.pyも置いてありますが jupyter notebok で見ることを前提にしています。
式を単純化するだけのコードです。計算結果はTEXで出しています。
運動方程式

各リンクのx軸とのなす角τ_0, τ_1は
$$\tau_0=\theta_0 ...(1-1)$$
$$\tau_1=\theta_0+\theta_1 ...(1-2)$$
です。 また、第一リンクの重心位置(x_0, y_0)は
$$\begin{bmatrix}x_0 \cr y_0\end{bmatrix}=\begin{bmatrix}l_{g0}cos\theta_0\cr l_{g0}sin\theta_0\end{bmatrix} ...(1-3)$$
で表せます。また、第二リンクの重心位置(x_1,y_1)は
$$\begin{bmatrix}x_1 \cr y_1\end{bmatrix}=\begin{bmatrix}l_{g0}cos\theta_0+ l_{g1}cos(\theta_0+\theta_1)\cr l_{g0}sin\theta_0+ l_{g1}sin(\theta_0+\theta_1)\end{bmatrix} ...(1-4)$$
で表せる。各リンクの運動エネルギー、位置エネルギー、損失エネルギー、一般化力をT_0, T_1, U_0, U_1, D_0, D_1, Q_0, Q_1、一般化座標q_0, q_1として、ラグランジュの運動方程式
$$ \frac{d}{dt}(\frac{\partial T}{\partial\dot q})-\frac{\partial T}{\partial q_i}+\frac{\partial U}{\partial q_i}+\frac{\partial D}{\partial \dot{q_i}}= Q_i (i =1,2) ...(1-5)$$
を用いて各リンクの運動方程式を求める。
ここで、一般化座標はq_i=θ_i (i=0,1)である。各リンクの慣性モーメントをI_0, I_1,関節の粘性摩擦係数をd_0, d_1としてT_0, T_1, U_0, U_1, D_0, D_1を求める。
$$T_0=\frac{1}{2} \left(I_{0} + l_{g0}^{2} m_{0}\right) \left(\frac{d}{d t} {q_{0}}{\left(t \right)}\right)^{2} ...(1-6)$$
$$U_0=g l_{g0} m_{0} \sin{\left({q_{0}}{\left(t \right)} \right)} ...(1-7)$$
$$D_0=\frac{d_{0} \left(\frac{d}{d t} {q_{0}}{\left(t \right)}\right)^{2}}{2} ...(1-8)$$
$$T_1=\frac{1}{2} I_{1} \left(\frac{d}{d t} {q_{0}}{\left(t \right)} + \frac{d}{d t} {q_{1}}{\left(t \right)}\right)^{2} \\+ \frac{1}{2} m_{1} \left(l_{0}^{2} \left(\frac{d}{d t} {q_{0}}{\left(t \right)}\right)^{2} + 2 l_{0} l_{g1} \cos{\left({q_{1}}{\left(t \right)} \right)} \left(\frac{d}{d t} {q_{0}}{\left(t \right)}\right)^{2} \\+ 2 l_{0} l_{g1} \cos{\left({q_{1}}{\left(t \right)} \right)} \frac{d}{d t} {q_{0}}{\left(t \right)} \frac{d}{d t} {q_{1}}{\left(t \right)} + l_{g1}^{2} \left(\frac{d}{d t} {q_{0}}{\left(t \right)}\right)^{2} \\+ 2 l_{g1}^{2} \frac{d}{d t} {q_{0}}{\left(t \right)} \frac{d}{d t} {q_{1}}{\left(t \right)} + l_{g1}^{2} \left(\frac{d}{d t} {q_{1}}{\left(t \right)}\right)^{2}\right) ...(1-9)$$
$$U_1=g m_{1} \left(l_{0} \sin{\left({q_{0}}{\left(t \right)} \right)} + l_{g1} \sin{\left({q_{0}}{\left(t \right)} + {q_{1}}{\left(t \right)} \right)}\right) ...(1-10)$$
$$D_1=\frac{d_{0} \left(\frac{d}{d t} {q_{1}}{\left(t \right)}\right)^{2}}{2} ...(1-11)$$
また、全体の運動エネルギー、位置エネルギー、損失エネルギーT, U, Dは
$$T=T_0+T_1 ...(1-12)$$
$$U=U_0+U_1 ...(1-13)$$
$$T=D_0+D_1 ...(1-14)$$
これより、
$$\frac{\partial T}{\partial \dot{q_0}}=I_{1} \left(\frac{d}{d t} {q_{0}}{\left(t \right)} + \frac{d}{d t} {q_{1}}{\left(t \right)}\right) + m_{1} \left(l_{0}^{2} \frac{d}{d t} {q_{0}}{\left(t \right)} \\+ 2 l_{0} l_{g1} \cos{\left({q_{1}}{\left(t \right)} \right)} \frac{d}{d t} {q_{0}}{\left(t \right)} + l_{0} l_{g1} \cos{\left({q_{1}}{\left(t \right)} \right)} \frac{d}{d t} {q_{1}}{\left(t \right)} + l_{g1}^{2} \frac{d}{d t} {q_{0}}{\left(t \right)} \\+ l_{g1}^{2} \frac{d}{d t} {q_{1}}{\left(t \right)}\right) + \left(I_{0} + l_{g0}^{2} m_{0}\right) \frac{d}{d t} {q_{0}}{\left(t \right)} ...(1-15)$$
$$\frac{d}{dt}(\frac{\partial T}{\partial \dot{q_0}})=I_{1} \left(\frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} + \frac{d^{2}}{d t^{2}} {q_{1}}{\left(t \right)}\right) + m_{1} \left(l_{0}^{2} \frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} \\- 2 l_{0} l_{g1} \sin{\left({q_{1}}{\left(t \right)} \right)} \frac{d}{d t} {q_{0}}{\left(t \right)} \frac{d}{d t} {q_{1}}{\left(t \right)} - l_{0} l_{g1} \sin{\left({q_{1}}{\left(t \right)} \right)} \left(\frac{d}{d t} {q_{1}}{\left(t \right)}\right)^{2} \\+ 2 l_{0} l_{g1} \cos{\left({q_{1}}{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} + l_{0} l_{g1} \cos{\left({q_{1}}{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} {q_{1}}{\left(t \right)} + l_{g1}^{2} \frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} \\+ l_{g1}^{2} \frac{d^{2}}{d t^{2}} {q_{1}}{\left(t \right)}\right) + \left(I_{0} + l_{g0}^{2} m_{0}\right) \frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} ...(1-16)$$
$$\frac{\partial T}{\partial q_0}=0 ...(1-17)$$
$$\frac{\partial U}{\partial q_0}=g \left(l_{g0} m_{0} \cos{\left({q_{0}}{\left(t \right)} \right)} + m_{1} \left(l_{0} \cos{\left({q_{0}}{\left(t \right)} \right)} + l_{g1} \cos{\left({q_{0}}{\left(t \right)} + {q_{1}}{\left(t \right)} \right)}\right)\right) ..(1-18)$$
$$\frac{\partial D}{\partial \dot{q_0}}=d_{0} \frac{d}{d t} {q_{0}}{\left(t \right)} ...(1-19)$$
$$∴ Q_0=I_{1} \left(\frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} + \frac{d^{2}}{d t^{2}} {q_{1}}{\left(t \right)}\right) + d_{0} \frac{d}{d t} {q_{0}}{\left(t \right)} \\+ g \left(l_{g0} m_{0} \cos{\left({q_{0}}{\left(t \right)} \right)} + m_{1} \left(l_{0} \cos{\left({q_{0}}{\left(t \right)} \right)} + l_{g1} \cos{\left({q_{0}}{\left(t \right)} + {q_{1}}{\left(t \right)} \right)}\right)\right) \\+ m_{1} \left(l_{0}^{2} \frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} - 2 l_{0} l_{g1} \sin{\left({q_{1}}{\left(t \right)} \right)} \frac{d}{d t} {q_{0}}{\left(t \right)} \frac{d}{d t} {q_{1}}{\left(t \right)} - l_{0} l_{g1} \sin{\left({q_{1}}{\left(t \right)} \right)} \left(\frac{d}{d t} {q_{1}}{\left(t \right)}\right)^{2} \\+ 2 l_{0} l_{g1} \cos{\left({q_{1}}{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} + l_{0} l_{g1} \cos{\left({q_{1}}{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} {q_{1}}{\left(t \right)} + l_{g1}^{2} \frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} \\+ l_{g1}^{2} \frac{d^{2}}{d t^{2}} {q_{1}}{\left(t \right)}\right) + \left(I_{0} + l_{g0}^{2} m_{0}\right) \frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} ...(1-20)$$
$$\frac{\partial T}{\partial \dot{q_1}}=I_{1} \left(\frac{d}{d t} {q_{0}}{\left(t \right)} + \frac{d}{d t} {q_{1}}{\left(t \right)}\right) \\+ l_{g1} m_{1} \left(l_{0} \cos{\left({q_{1}}{\left(t \right)} \right)} \frac{d}{d t} {q_{0}}{\left(t \right)} + l_{g1} \frac{d}{d t} {q_{0}}{\left(t \right)} + l_{g1} \frac{d}{d t} {q_{1}}{\left(t \right)}\right) ...(1-21)$$
$$\frac{d}{dt}(\frac{\partial T}{\partial \dot{q_1}})=I_{1} \left(\frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} + \frac{d^{2}}{d t^{2}} {q_{1}}{\left(t \right)}\right) + l_{g1} m_{1} \left(- l_{0} \sin{\left({q_{1}}{\left(t \right)} \right)} \frac{d}{d t} {q_{0}}{\left(t \right)} \frac{d}{d t} {q_{1}}{\left(t \right)} \\+ l_{0} \cos{\left({q_{1}}{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} + l_{g1} \frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} + l_{g1} \frac{d^{2}}{d t^{2}} {q_{1}}{\left(t \right)}\right) ...(1-22)$$
$$\frac{\partial T}{\partial q_1}=- l_{0} l_{g1} m_{1} \left(\frac{d}{d t} {q_{0}}{\left(t \right)} + \frac{d}{d t} {q_{1}}{\left(t \right)}\right) \sin{\left({q_{1}}{\left(t \right)} \right)} \frac{d}{d t} {q_{0}}{\left(t \right)} ...(1-23)$$
$$\frac{\partial U}{\partial q_1}=g l_{g1} m_{1} \cos{\left({q_{0}}{\left(t \right)} + {q_{1}}{\left(t \right)} \right)} ...(1-24)$$
$$\frac{\partial D}{\partial \dot{q_1}}=d_{0} \frac{d}{d t} {q_{1}}{\left(t \right)} ...(1-25)$$
$$∴ Q_1= I_{1} \frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} + I_{1} \frac{d^{2}}{d t^{2}} {q_{1}}{\left(t \right)} + d_{0} \frac{d}{d t} {q_{1}}{\left(t \right)} +\\ g l_{g1} m_{1} \cos{\left({q_{0}}{\left(t \right)} + {q_{1}}{\left(t \right)} \right)} + l_{0} l_{g1} m_{1} \sin{\left({q_{1}}{\left(t \right)} \right)} \left(\frac{d}{d t} {q_{0}}{\left(t \right)}\right)^{2} +\\ l_{0} l_{g1} m_{1} \cos{\left({q_{1}}{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} + l_{g1}^{2} m_{1} \frac{d^{2}}{d t^{2}} {q_{0}}{\left(t \right)} + l_{g1}^{2} m_{1} \frac{d^{2}}{d t^{2}} {q_{1}}{\left(t \right)} ...(1-26)$$
以上を行列式の形にすると、
$$\begin{bmatrix}Q_0 \cr Q_1\end{bmatrix}=\\ \begin{bmatrix}I_0+m_0l_{g0}^2+I_1+m_1(l_0^2+l_{g1}^2+2l_0l_{g1}cos\theta_1)& I_1+m_1(l_{g1}^2+l_0l_{g1}cos\theta_1)\cr I_1+m_1(l_{g1}^2+l_0l_{g1}cos\theta_1)& I_1+m_1 l_{g1}^2\end{bmatrix}\begin{bmatrix}\ddot{\theta_0} \cr \ddot{\theta_1}\end{bmatrix}\\+\begin{bmatrix}d_0& 0\cr 0& d_1\end{bmatrix}\begin{bmatrix}\dot{\theta_0} \cr \dot{\theta_1}\end{bmatrix}\\+\begin{bmatrix}-m_1l_0l_{g1}(2\dot{\theta_0}\dot{\theta_1}+\dot{\theta_1}^2)sin\theta_1& m_0gl_{g0}cos(\theta_0)+m_1g(l_{0}cos\theta_0+l_{g1}cos(\theta_0+\theta_1))\cr m_1l_0l_{g1}\dot{\theta_0}^2sin\theta_1& m_1gl_{g1}cos(\theta_0+\theta_1)\end{bmatrix} \\...(1-27)$$
参考資料と一致しました。OK!! (雑記2.)
simplyfy式変形後は順番がめちゃくちゃなので綺麗に行列の形に直すのはかなり面倒です。気をつけてください。(雑記3.)
ここまでの参考
シミュレーション
動く図を作っていきます。
順運動学と逆運動学
第二リンクの先端位置(x_0,y_0)は
$$\begin{bmatrix}x_0 \cr y_0\end{bmatrix}=\begin{bmatrix}l_{0}cos\theta_0\cr l_{0}sin\theta_0\end{bmatrix} ...(2-1)$$
第二リンクの先端位置(x_1,y_1)は
$$\begin{bmatrix}x \cr y\end{bmatrix}=\begin{bmatrix}x_1 \cr y_1\end{bmatrix}=\begin{bmatrix}l_{0}cos\theta_0+ l_{1}cos(\theta_0+\theta_1)\cr l_{0}sin\theta_0+ l_{1}sin(\theta_0+\theta_1)\end{bmatrix}...(2-2)$$
これを解いていきます。移項して,
$$x-l_{0}cos\theta_0= l_{1}cos(\theta_0+\theta_1)...(2-3)$$
$$y-l_{0}sin\theta_0= l_{1}sin(\theta_0+\theta_1) ...(2-4)$$
どちらも両辺2乗し、2式を足し合わせます。
$$x^2+y^2+l^2_0-2l_0(xcos\theta_0+ysin\theta_0)=l^2_1...(2-5)$$
cos,sinに関してまとめると,
$$\sqrt{x^2+y^2}cos(\theta_0+\alpha)=\frac{x^2+y^2+l^2_0-l^2_1}{2l_0}...(2-6)$$
ただし,
$$tan( \alpha)=\frac{y}{x}...(2-7)$$
$$∴ \theta_0=-\alpha\pm cos^{-1}(\frac{x^2+y^2+l^2_0-l^2_1}{2l^2_0\sqrt{x^2+y^2}})...(2-8)$$
次にθ_1を求めます。
(2-3)/(2-4)より,
$$\frac{y-l_{0}sin\theta_0}{x-l_{0}cos\theta_0}=tan(\theta_0+\theta_1)...(2-9)$$
$$∴\theta_1=-\theta_0+tan^{-1}(\frac{y-l_{0}sin\theta_0}{x-l_{0}cos\theta_0})...(2-10)$$
- 参考
2-2.【Python】2リンクマニピュレータの逆運動学シミュレーション -西住工房
2-3.大分大学工学部福祉環境工学科メカトロニクスコース松尾研究室ゼミ資料"MATLAB による 2 リンクロボットマニピュレータ制御のシミュレーション"
順逆運動学計算用コード
- そも
%matplotlib inline
%matplotlib notebookって何ですか、ということ。jupyter内で図を見えてくれるinlineは良く使います。使わなくても出るような気がするけど、出ない時にはとりあえず書き加える感じ。
一方notebookは編集可能らしい。アイコンをタッチしてから右クリックでドラッグしたり、いろんな操作ができ図を弄れる、上の電源ボタンみたいなもので画像を固定できる。
=>参考2-1、2-2
- wedget
公式のUsing~を見てみます。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
@interact(amp=(0.1, 4.0, 0.1), omega=(0.1, 4.0, 0.1), phase=(-np.pi, np.pi, 0.1),
fn = {'sin': np.sin, 'cos': np.cos, 'tan': np.tan})
def h(amp=1.0, omega=1.0, phase=0.0, fn=np.sin):
domain=[-np.pi, np.pi]
x = np.linspace(domain[0], domain[1], 100)
y = amp * fn(omega * x + phase)
plt.plot(x, y)
plt.plot(-phase/omega, 0, 'or')
plt.xlim(domain)
plt.ylim([-4, 4])
x=(最小,最大,ステップ)はinteractでも設定でき、初期設定としてinteractを使用したい場合はデコレータとして使用出来る。辞書型で与えると選択肢に出来る。
- コード 2
https://github.com/inomatly/robot_arm/blob/master/arm_sim.ipynb
一応.pyも置いてありますが jupyter notebok で見ることを前提にしています。
動いている様子:
楽しい。でもめっちゃ重い。(雑記3.)
このとき、(2-9)の±によって解(すなわち姿勢)は2通りあります。たとえば(1,1)は間接が(1,0)にある場合と(0,1)にある場合が考えられます。今回は計算を簡単にする為に1通りに統一しています。
特異点に関して
ヤコビ行列=0になるような姿勢は特異姿勢と呼ばれ、その点は特異点と呼ばれる。
(1)式を微分するとヤコビ行列Jは
$$\begin{bmatrix}\dot{x} \cr \dot{y}\end{bmatrix}=\begin{bmatrix}-l_{0}sin\theta_0 - l_{1}sin(\theta_0+\theta_1) & - l_{1}sin(\theta_0+\theta_1) \cr l_{0}cos\theta_0+ l_{1}cos(\theta_0+\theta_1) & l_{1}cos(\theta_0+\theta_1)\end{bmatrix}\begin{bmatrix}\dot{\theta_0} \cr \dot{\theta_1}\end{bmatrix}...(1)$$
$$∴ J=\begin{bmatrix}-l_{0}sin\theta_0 - l_{1}sin(\theta_0+\theta_1) & - l_{1}sin(\theta_0+\theta_1) \cr l_{0}cos\theta_0+ l_{1}cos(\theta_0+\theta_1) & l_{1}cos(\theta_0+\theta_1)\end{bmatrix}$$
特異点では
$$det J = l_0l_1sin\theta_1=0$$
$$∴ \theta_1=n\pi$$
n=0,1,2。この場合、たとえば(x,y) = (-2/√2,-2/√2)の伸びきった姿勢のような姿勢や、(0,0)のような縮こまった姿勢を示します。それ以上伸びたり縮んだり出来ない出来ませんから、一般に特異点では自由度が下がってることになります。
目標点が特異点を通る場合は問題ありませんが、特異点付近を通るときはアームが急激に動くため注意が必要です。(雑記5.)=>2-3
参考 2
2.1 Jupyter Notebookにおけるmatplotlib -Pythonオンライン学習サービスPyQ(パイキュー)
2-2 jupyter notebookにmatplotlibを使ってグラフを描画する -山本隆の開発日誌
2-3「ロボット工学 ー機械システムのベクトル解析ー, 広瀬茂男著 裳華房 2003年」の10章
雑記
- コードに関して、「pythonじゃなくてmatlabとかmathematicaでいいんじゃないの」とも思いますが。新しく覚えるおが面倒なのと、学生のうちは安価ですが将来的には金がかかりますのでなるべくオープンソースを使っていきたいという意思表示です。オープンソース贔屓です。判官贔屓的な。
- 「まだ微分で消耗してるの?」正月休みの1/3に手でゴリゴリ計算して、参考にしたのが正しいっぽいことを確認してからコード書いたので二度手間ですが、今後はラグランジュ方程式を使いまわせるのでOKということにしました。TEXコードまで出してくれるの神ですね。禁断の果実という感じがします。
- ラグランジュ方程式は使えるようになったかな(わからないけど)と思いますが、お恥ずかしながらベクトル的な解法に苦手意識があります。これからやっていきたいと思います。
- シミュレーションは、jupyter上の位置の問題なのか、かくかくしますね。難しい。動かしているときめっちゃチカチカするのは何故なのか。計算が重いんだろうか?だれかプログラミングおしえて。
- ひよこの真似やワクワクっ!な動作のように脇を開閉する動きはこの類い...ではないですね。人間の腕は自由度のバケモノですから。ワクワクの時の手首が特異点かと言えばそんなわけない。
