月: 2019年2月

pythonでグラフを表示するまでの流れを紹介します。グラフは自由振動、減衰振動、強制振動、倒立振り子(倒立振子、縦棒制御)の制御っぽいことをして時間変化をグラフで表示しました。おまけでCR回路の電圧の充電具合をプロットしました。 グラフを表示するのはCとかでも簡単にできますが、機械学習やってみたいのでpythonに触れる機会にします。

目次

• 目的
• グラフの様子
• pythonとは
• 環境とインストール
• Jupyter Notebookの使い方
• 振動の基礎とコード
• 倒立振り子の運動方程式
• 雑記
• 参考

目的

思いのままのグラフを表示します。多項式だけではなく行列やベクトル、微分方程式も扱えるようになりたいと思います。

グラフの様子

今回は2つの似たような数式モデルをプロットしました。

• 倒立振り子(縦棒制御)

手の上で箒のバランスを取るやつです。振動の中でも強制振動です。ニュートンの運動方程式を立てると、次のようになります。振り子は2l[m]、棒はm[kg]、台車はM[kg]です。このとき、角度Θを十分に小さいとして 近似してかなり簡単な式にまとめてあります。導出過程はページ最後に書きました。

$$\dot \theta_1(t)=\theta_2 \\ \dot \theta_2(t) = \frac{3}{l(4M+m)}(-L\theta_2+{g(M+m)-K}\theta_1)$$

簡単のためにl=1[m],M=2/3[kg],m=1/3[kg]を選ぶと、

$$\dot \theta_1(t)=\theta_2 \\ \dot \theta_2(t) = -L\theta_2+(g-K)\theta_1$$

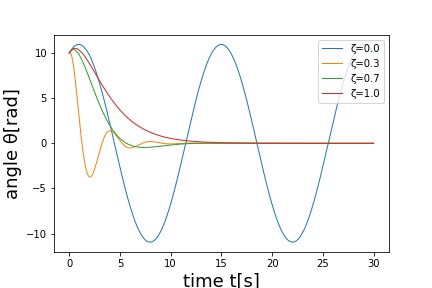
この式で常微分方程式を解くと下記のような美しいグラフに！！コードが汚いのは御愛嬌ということで。python初めてだったのでほぼパクリです。減衰比については振動の基礎の項目に軽く書いています。

from sympy import *      # sympyライブラリから全ての機能をimoprt
import numpy as np       #ベクトルや行列を表すのに使うライブラリnumpy
from scipy.integrate import odeint #scipyに含まれる常微分方程式を解く関数
import matplotlib.pyplot as plt　#グラフを書くためのライブラリ
%matplotlib inline 　　　　#jupyter notebook内で表示させるため

"""
2階微分方程式 倒立振子 
"""
#シンボル定義
x=Symbol('x')                  # 文字'x'を変数xとして定義
t=Symbol('t')                  # 文字 't'を変数tとして定義

g = 9.8     #重力加速度
La = 0.89   #減衰比0.7のグラフのフィードバックゲイン
Ka = 10.2  
Lb = 1.0    #減衰比1.0のグラフのフィードバックゲイン
Kb = 10.05  
Lc = 0.0    #減衰比0.0のグラフのフィードバックゲイン
Kc = 10.0   
Ld = 1.0    #減衰比0.3のグラフのフィードバックゲイン
Kd = 12.57  

def func1(x, t, K):
    x1,x2=x
    dxdt=[x2,(-La*x[1])+((g-Ka)*x[0])]
    return dxdt
#同じことを複数書いているので省略

x0 = [10.0,2.0] # 初期条件　[x(0), dx(0)/dt]を表す

t=np.linspace(0,30,1000) # 時間 0から10までを101等分する
sol1=odeint(func1, x0, t, args=(k,)) # 微分方程式を解く 
#同じことを複数書いているので省略

#グラフ表示
plt.plot(t, sol3[:,0], linewidth=1,label='ζ=0.0') #  角度を図示。
plt.xlabel('time t[s]', fontsize=18)
plt.ylabel('angle θ[rad]', fontsize=18)
plt.legend(loc='upper right')
plt.savefig('huriko1.jpg')
plt.show()

• LCR回路

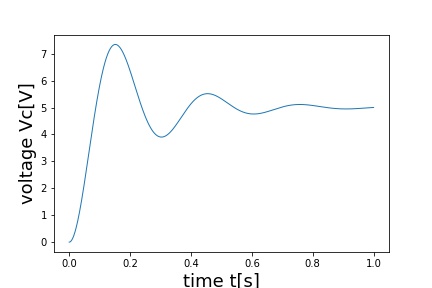
そしてもう一つの式がこれです。回路のキャパシタはダンパー、インダクタはばねと同じです。

$$ E = v_R + v_C + v_L \\ E = L\frac{di(t)}{dt}+Ri(t)+\frac{1}{C}\int i(t)dt $$

これをキャパシタ電圧でまとめると

$$ i = C\frac{d}{dt}v_C \\ \frac{d^2}{dt^t} v_c = -\frac{R}{C} \frac{d}{dt}v_c -\frac{1}{LC}v_c + \frac{E}{LC}$$

これは強制振動の式と同じ形なので、同じようなグラフがかけます。

python とは

今回のpythonは読みやすく、それでいて効率もよいコードをなるべく簡単に書けるように作られたプログラミング言語です。言語自体も書きやすいように作られていますが、ライブラリやワーススペースが豊富で、だいたい何でも出来るみたいです。最近ではAIや機械学習が人気ですが、そういう事をするためのライブラリが豊そろっているみたいで、最近活躍している言語です。 2系と3系は全然違うので注意が必要です。

ライブラリというのは、

ライブラリとは、複数のプログラムが共通して利用するコードをまとめたファイルである。 ライブラリ自体は単独で実行することはできない。 from I-8-8. ライブラリとプログラムの関係 | 日本OSS推進フォーラム

というものです。必要なときに呼び出すと自分の仕事だけやって帰って行きます。

ちなみに、初学者へ。世の中のホームページやアプリの画面表示は別な言語で書いています。pythonとかCとかは計算処理をやってくれるものなので、これだけやっても画面表示は出来ません。注意してください。勉強しはじめたころの私はこのあたりよく分かって無かったために時間が掛かってしまったので一応書いておきました。

環境とインストール

環境はAnacondaでまとめてインストールしてJupyter Notebookで書きます。 python公式でインストールしても良いんですが、他にもいろいろまとめてインストール出来るらしいDownloads - Anacondaでインストールした方が楽みたいです。デフォルトのままで良いので指示に従うだけです。

Jupyter Notebookの使い方

インストールしたらJupyterNotebookを起動します。するとコマンドコマンドプロンプト（っぽいなにか）が出てきますので、そこに書かれているURLをブラウザで開いてください。

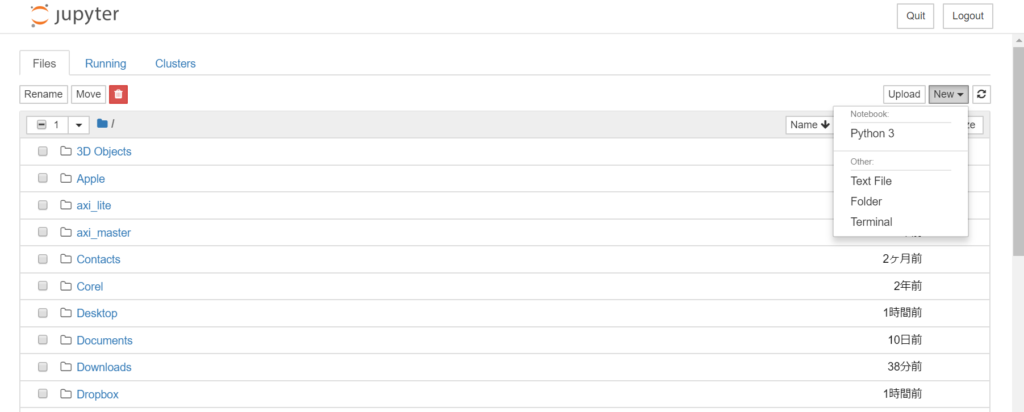
ユーザーのフォルダの中身が表示されますので、好きなのを選んで右上のnewからpython3をクリック。すると、プログラムを書くためのセルが出てきます。

今数字が書いてある色塗りの部分を押すとコマンドモードになり数式やらがかけます。In[]やOut[]と書いている部分はエディットモードで、コピーやらが出来ます。エディットモードでHを押すとヘルプが出ます。

コマンドモードで上のcodeの部分をmorkdownにすると、morkdownで文章を書けます。 morkdownは私がこのブログの下書きやメモに普段使いしているマークアップ言語(HTMLの仲間)で、# ABC　と書くとタイトル的な大きな文字、## ABCと書くと1段階小さい文字、なにもつけないと普通の文字、- と書くと箇条書き、というようにかなり使いやすい言語です。

pythonの記法はすっ飛ばします。numpyというライブラリを読みこんでベクトル(1次元配列)や行列（2次元配列）を表せます。 スライシング。bool。

コマンドプロンプトでサーバーをlocalhostで立てて、ブラウザで表示しているんじゃないかと思います（このあたりよく解ってませんが。たぶん。。なので、ブラウザで開いている間にJupyterNotebookを消すとエラーをはきます。

発生したエラーについて

• 保存した画像が真っ白になっている。jupyterにはグラフが出力されている

Python matplotlibのグラフが保存できない(windows+anaconda) teratail

• 自然数ってどうやるの 【Python】ネイピア数をグラフにプロットする -qiita

振動の基礎とコード

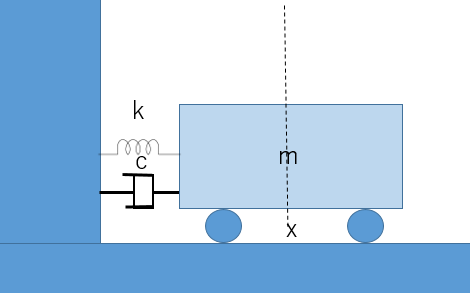
機械屋さんにとってのかなり基本的なモデル（らしい）で考えます。ニュートンの運動方程式を立てます。

$$ f(t)= m\frac{d^2x(t)}{dt^2}+c\frac{dx(t)}{dt}+kx(t) $$

これは強制振動を表しています。

振動は、自由振動、減衰振動、強制振動の3つに分けられます。自由振動は正弦波などのように振動し続けます。減衰振動は自由振動が次第に減衰していきます。強制振動は減衰振動に外力を加えている場合です。 日常生活では大概空気抵抗などで減衰するので減衰振動がイメージしやすいかと思います。一方、制御するときはモータが動いているので強制振動です。

外力をf(t)と書いていますから、f(t)＝0なら減衰振動、f(t)の項が有れば強制振動になります。

上の式を作為的に以下のように変形します。

$$ f(t)= \frac{d^2x(t)}{dt^2}+2\zeta\omega_n\frac{dx(t)}{dt}+\omega_n^2 \ \\減衰比\zeta = \frac{c}{2\sqrt{km}}, 固有振動数\omega_n = \sqrt{\frac{k}{m}} $$

減衰比ζは減衰具合、固有振動数ω_nは振動時の周波数に対応しています。これが減衰振動の基本的なモデルです。ζ=0のとき全く減衰しないのでsin波のような自由振動をし、ζ=1の時過不足無く（クッションに沈むように）目標値に到達します。実際には誤差や外乱が入るので制御系を作るときには0.7くらいにするそうです。

今回はpythonで解きたいので、ここから変形していきます。本当はいろんな方法が有るみたいなんですが、そのうちやると言うことにして、今回は参考本と同じ方法で解いていきたいと思います。

常微分方程式を解きます。二次方程式は大変なので、以下のように書きかえます。

$$\frac{dx_1(t)}{dt}=x_2 \\ \frac{dx_2(t)}{dt} = -\frac{c}{m}x_2-\frac{k}{m}x_1 +f(t)$$

これを行列を用いたベクトル表現にすると、

$$ \frac{d}{dt} \left[ \begin{array}{rrr} x_1 \\ x_2 \end{array} \right] = \left[ \begin{array}{rrr} 0 \ & 1 \ \\ -\frac{k}{m} & -\frac{c}{m} \\ \end{array} \right] \left[ \begin{array}{rrr} x_1 \\ x_2 \end{array} \right] + \left[ \begin{array}{rrr} 0 \\ 1 \end{array} \right] f(t)$$

この式のように変数の位置x(t)を配列としてpythonで定義すると、以下のようになります。

m = 1.0 #質量
c = 0.5 #粘性減衰
k = 1.0 #ばね定数

def func(x, t, k):
    x1,x2=x
    dxdt=[x2,-c/m*x[1]-k/m*x[0]+sin(t/2)]
    return dxdt

x0 = [0.0,0.0] # 初期条件　[x(0), dx(0)/dt]を表す.今は初速０．

t=np.linspace(0,50,100000) # 時間　0から10までを101等分する
sol=odeint(func, x0, t, args=(k,)) # 数値的に微分方程式を解き， x(t)とx'(t)をsolのリストの[:,0]、[:,1]成分へ格納する。

以上のような感じで、パラメータをいじることで自由振動、減衰振動、強制振動がそれぞれ再現出来ました。

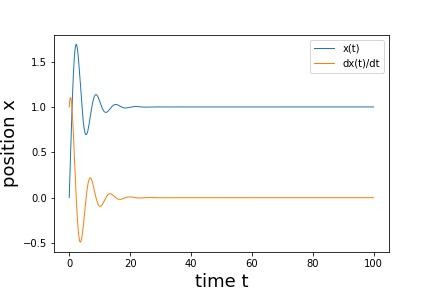
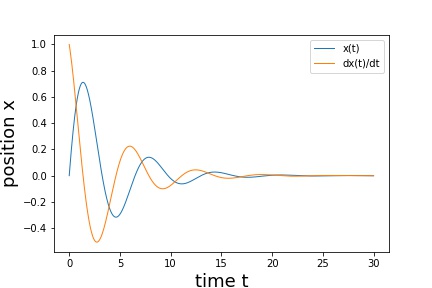
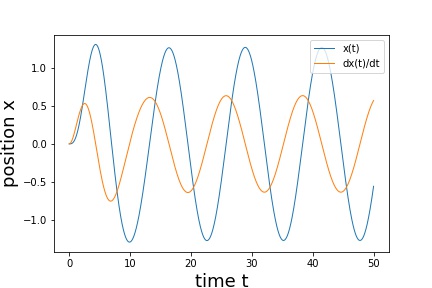
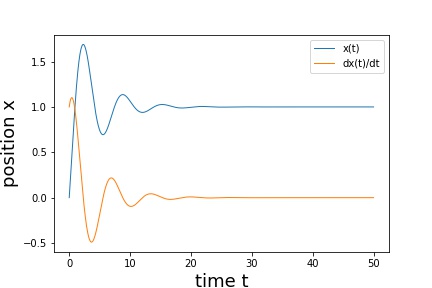
• 自由振動（図5）　初期x=0.0, 初期x' = 1.0, m = 1.0, c = 0.0, k = 1.0
• 減衰振動（図6）　初期x=0.0, 初期x' = 1.0, m = 1.0, c = 0.5, k = 1.0
• 強制振動（図7）　初期x=0.0, 初期x' = 0.0, m = 0.0, c = 0.5, k = 1.0 f(t) = sin(t/2)
• 強制振動（図8）　初期x=0.0, 初期x' = 0.0, m = 1.0, c = 0.5, k = 1.0 f(t) = 1

倒立振り子の運動方程式

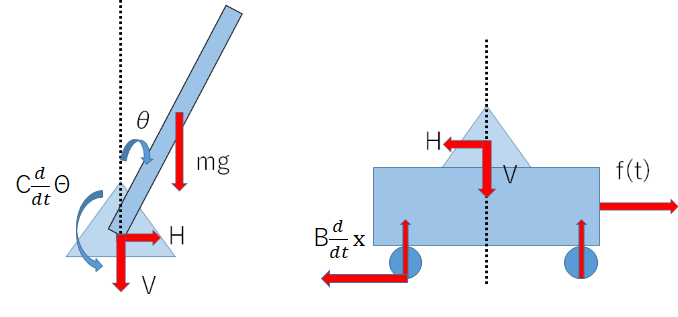
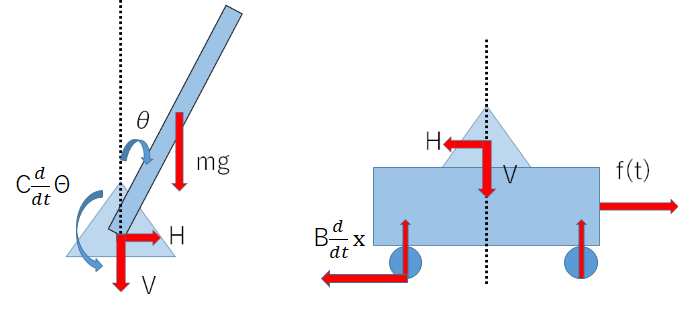
台車と振り子を図に示します。 粘性摩擦係数をB、 軸の粘性摩擦係数をCとおきました。ここから、下の4つの式が立てられます。

振り子について

$$J\ddot \theta = Vlsin\theta - Hlcos \theta - C\dot \theta …(1)\\ (J=\frac{ml^2}{3})\\ m\frac{d^2}{dt^2}(x + lsin\theta)= H…(2) \\ m\frac{d^2}{dt^2}(lcos\theta)=V - mg…(3)$$

台車について

$$M \ddot x = f(t) - B \dot x - H…(4)$$

簡単のためにC = 0, B = 0とします。ここからH,Vを消去します。

$$H = m \ddot x + ml \ddot \theta sin\theta - ml (\dot \theta)^2 sin\theta…(5) \\ V = -ml \ddot \theta sin \theta - ml(\dot \theta) cos \theta +mg…(6)$$

これを(1)(4)に代入してまとめると、

$$ J\ddot \theta= -ml^2 \ddot \theta - lmcos\theta \ddot x + mglsin\theta…(7) \\ (M+m) \ddot x = -ml\ddot \theta cos\theta + ml(\dot \theta)^2 sin\theta+f(t)…(8)$$

この式からxの2階微分を消去して、Θが十分小さいとして線形化すると

$$cos\theta\approx 1,sin\theta\approx\theta, (\theta)^2 \approx 0 \\ \ddot \theta l (4M+m)-3(M+m)g \theta = -3f(t)…(9)$$

f(t)に角度と各速度についてフィードバックさせます。

$$ f(t)= L \dot \theta + K \theta\ $$

簡単のために l = 1[m], M = 2/3[kg], m = 1/3[kg]とおくと、以下のようにかけます。プログラムで解けるように一階化します。

$$ \dot \theta_1 = \theta_2 \\ \dot \theta_2 = -L \theta_2 + (g-K)\theta_1$$

一応全体の全体をラプラス変換して伝達関数の式を求めます。（せっかく導出したから書きたい。）

$$L{\theta(t)}=\Theta(s),L{f(t)}=F(s)として\\ \frac{\Theta(s)}{F(s)}=\frac{-3}{(4M+m)ls^2+3ls-3(M+m)g+K}$$

雑記

プログラミング系のサイトは最近公開されたものを見るように気をつけるようになりました。機械系や電気系の、特に理論はかなり成熟しているのでふるいサイトでも何でも読みやすくわかりやすければ良いんですが、情報系はツールがどんどん更新されていくので最新のを見ないと妙なところで躓いてしまいます。 おかげで私のPCちゃんはパスとかアプリとか訳が分からない感じになっています。情報系の特にweb系のブロガーさんは情報収集がすごいので、最新のでも誰かしら先にやっていますので安心ですね。先人は偉大です。 それと、解析力学が難しいですね。もう少し時間をかけないとわからないです。ラグランジュ難しい。制御はやって行きたいので、のんびり本を読んでいきます。
追記(2019/3/20)参考リンクをリストにしました。Amazonリンクを増やしました。

参考

• 短期集中:振動論と制御理論 工学系の数学入門 吉田勝俊　日本評論社
• Pythonで動かして学ぶ！ あたらしい機械学習の教科書　伊藤真　翔泳社
• 現場で役立つ制御工学の基本　涌井伸二・橋本誠二・高梨宏之・中村幸紀　コロナ社
• 倒立振子の制御
• Windows(MS)にPython(Anaconda)を導入する（6つの罠）-qiita
• matplotlibで作成したプロットを画像ファイルに保存する方法 -qiita
• [Pythonによる科学・技術計算] 2階常微分方程式の数値解法，初期値問題，数値計算 -qiita
• 一様な棒の慣性モーメントの計算方法と考察 -具体例で学ぶ数学
• とつとつとしてろうとせず -Hatena Blog